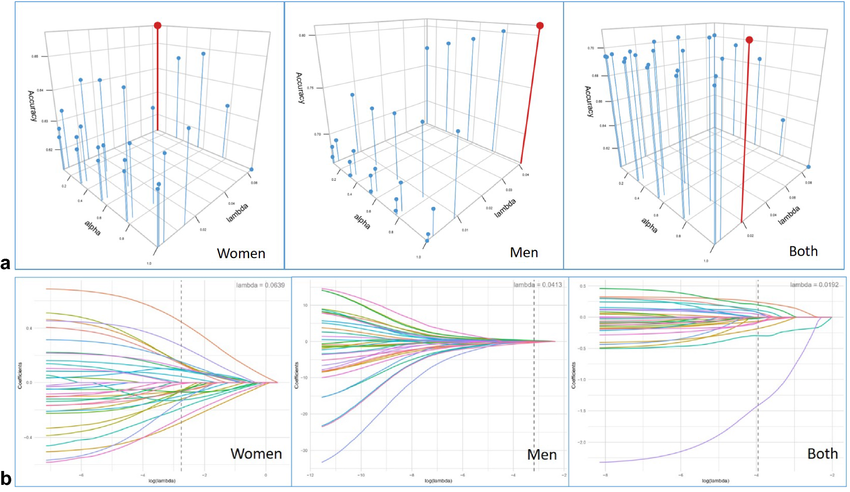
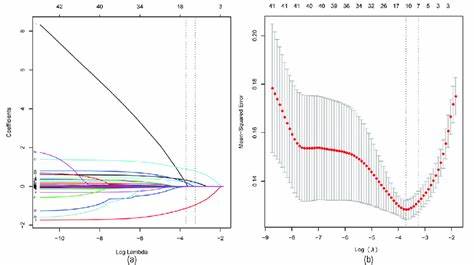
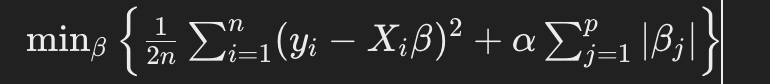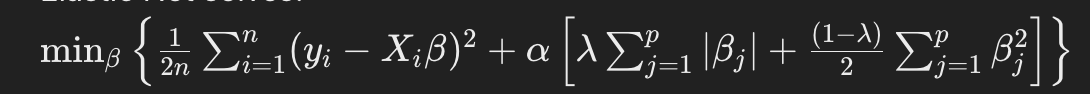Regularization.
Regularization TechniquesRegularization techniques like Lasso and Elastic Net are crucial in handling high-dimensional data, preventing overfitting, and improving model generalization.
Lasso Regression (L1 penalty)
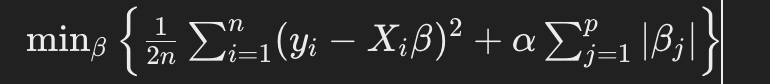 : Adds a penalty equal to the absolute value of the magnitude of coefficients. It can zero out some coefficients, effectively performing feature selection.
: Adds a penalty equal to the absolute value of the magnitude of coefficients. It can zero out some coefficients, effectively performing feature selection.
Elastic Net Regression (L1 and L2 penalties)
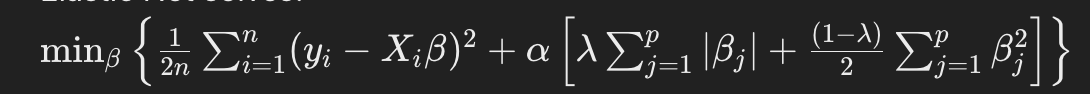 Combines both L1 and L2 penalties, balancing between Lasso and Ridge regression. It’s particularly useful when dealing with correlated features.
Combines both L1 and L2 penalties, balancing between Lasso and Ridge regression. It’s particularly useful when dealing with correlated features.
Lasso Regression Lasso solves the optimization problem
Elastic Net Regression
Data Preparation
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
# Load your dataset
data = pd.read_csv('your_dataset.csv')
X = data.drop('target', axis=1)
y = data['target']
# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
Advanced Feature Engineering Consider techniques like polynomial features, interaction terms, and scaling.
from sklearn.preprocessing import StandardScaler, PolynomialFeatures
# Generate polynomial and interaction features
poly = PolynomialFeatures(degree=2, include_bias=False)
X_train_poly = poly.fit_transform(X_train)
X_test_poly = poly.transform(X_test)
# Standardize the features
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train_poly)
X_test_scaled = scaler.transform(X_test_poly)
Advanced Model Implementation, Lasso with Cross-Validation
Using cross-validation to find the optimal α\alphaα.
from sklearn.linear_model import LassoCV
from sklearn.metrics import mean_squared_error
# Lasso with cross-validation
lasso_cv = LassoCV(cv=10, random_state=42)
lasso_cv.fit(X_train_scaled, y_train)
# Best alpha
print(f'Optimal alpha for Lasso: {lasso_cv.alpha_}')
# Predictions and evaluation
y_pred_lasso = lasso_cv.predict(X_test_scaled)
mse_lasso = mean_squared_error(y_test, y_pred_lasso)
print(f'Lasso MSE: {mse_lasso}')
Elastic Net with Cross-Validation Using cross-validation to find the optimal
from sklearn.linear_model import ElasticNetCV
# Elastic Net with cross-validation
elastic_net_cv = ElasticNetCV(cv=10, random_state=42)
elastic_net_cv.fit(X_train_scaled, y_train)
# Best parameters
print(f'Optimal alpha for Elastic Net: {elastic_net_cv.alpha_}')
print(f'Optimal l1_ratio for Elastic Net: {elastic_net_cv.l1_ratio_}')
# Predictions and evaluation
y_pred_enet = elastic_net_cv.predict(X_test_scaled)
mse_enet = mean_squared_error(y_test, y_pred_enet)
print(f'Elastic Net MSE: {mse_enet}')
Hyperparameter Tuning using Grid Search For more granular control over hyperparameters:
from sklearn.model_selection import GridSearchCV
# Define parameter grid
param_grid = {
'alpha': [0.01, 0.1, 1, 10, 100],
'l1_ratio': [0.1, 0.5, 0.9]
}
# Elastic Net Grid Search
elastic_net_grid = GridSearchCV(ElasticNet(), param_grid, cv=10, scoring='neg_mean_squared_error')
elastic_net_grid.fit(X_train_scaled, y_train)
print(f'Best parameters from Grid Search: {elastic_net_grid.best_params_}')
print(f'Best score from Grid Search: {elastic_net_grid.best_score_}')
# Predictions and evaluation
best_enet = elastic_net_grid.best_estimator_
y_pred_best_enet = best_enet.predict(X_test_scaled)
mse_best_enet = mean_squared_error(y_test, y_pred_best_enet)
print(f'Best Elastic Net MSE from Grid Search: {mse_best_enet}')
Feature Selection and Model Interpretation Coefficient Analysis
After fitting the model, analyzing coefficients can help understand feature importance.
import matplotlib.pyplot as plt
# Lasso coefficients
lasso_coefs = lasso_cv.coef_
plt.plot(range(len(lasso_coefs)), lasso_coefs)
plt.title('Lasso Coefficients')
plt.show()
# Elastic Net coefficients
enet_coefs = best_enet.coef_
plt.plot(range(len(enet_coefs)), enet_coefs)
plt.title('Elastic Net Coefficients')
plt.show()
Model Deployment and Advanced Inference Saving the Model
You can use joblib to save the trained model for later use.
import joblib
# Save the best Elastic Net model
joblib.dump(best_enet, 'best_elastic_net_model.pkl')
# Load the model for inference
loaded_model = joblib.load('best_elastic_net_model.pkl')
# Make predictions with the loaded model
loaded_predictions = loaded_model.predict(X_test_scaled)
Practical Considerations Handling Multicollinearity
Elastic Net is particularly useful in the presence of multicollinearity. It can handle correlated predictors better than Lasso by combining L1 and L2 penalties.
Choosing the Right Model Lasso: Preferable when you expect a few non-zero coefficients (sparse solution). Elastic Net: Preferable when you expect many correlated features. Model Interpretation
 Clothes Try-On
Convolutional Networks
Clothes Try-On
Convolutional Networks
 CNN GANS
BRAND & PRODUCT 3D RENDER
Text to Video.
CNN GANS
BRAND & PRODUCT 3D RENDER
Text to Video.
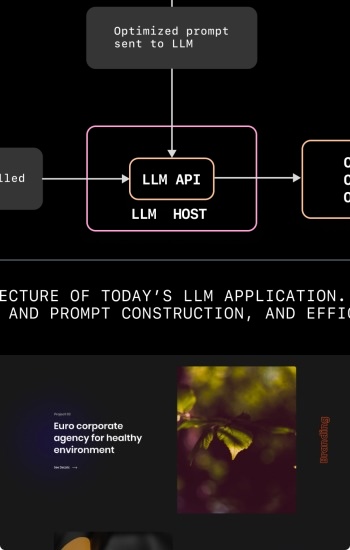 LLM'S NPL-TRY
Fine-tunning Transformers
LLM'S NPL-TRY
Fine-tunning Transformers
 Elastic Net Lasso
INFERENCE LLMS
Elastic Net Lasso
INFERENCE LLMS
 LSTM
difussion transformers
LSTM
difussion transformers
 Caption music tracks
Text to music.
Caption music tracks
Text to music.